
 We have just seen that
the Biot-Savart Law is in some sense the magnetic equivalent of
Coulomb's Law. Is there a magnetic equivalent of Gauss's
Law ? The answer is (of course) yes - Ampere's Law.
We have just seen that
the Biot-Savart Law is in some sense the magnetic equivalent of
Coulomb's Law. Is there a magnetic equivalent of Gauss's
Law ? The answer is (of course) yes - Ampere's Law. 
where ds is an element of length around an arbitrary closed loop "C", called an Amperian loop and the summation is over all currents passing through the loop.
Currents passing "out of" the loop are defined as positive, currents passing into the loop are negative, whereas current which do not pass through the loop are not included in the summation.
Ampere's Law forms part of the second of Maxwell's equations. We will shortly adjust it slightly (following Maxwell), to complete the second of Maxwell's equations. Remember, Gauss's Law was the first of Maxwell's equations.
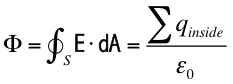
Note that Gauss's Law involves a surface integral of E over a closed Gaussian surface "S". Ampere's Law involves a line integral around a closed Amperian loop "C".
Gauss's Law is valid for any arbitrary closed Gaussian surface. Similarly Ampere's Law is valid for any closed (Amperian) loop.

 Symmetry argument:
Symmetry argument:
Since the wire is infinite, we know from the
Biot-Savart Law that B is perpendicular to dl
and r and thus lines of B must form
concentric circles around the current. Also, B
can, at most, depend only on the distance from the
wire, r.
The Amperian loop is chosen so that B is constant on the loop and in the same direction as ds - that is a circle whose plane is perpendicular to the wire and centered on the wire. This allows us to take B "out of the integral".
With the Amperian loop above we have



 B due to
an infinite solenoid
B due to
an infinite solenoid
Since the solenoid is infinite, we conclude that B
is directed along the axis of the solenoid.
Also, B can, at most, depend only on the
distance from the axis of the solenoid. For an
infinite solenoid B = 0 outside the solenoid.
 Choice of Amperian Loop:
Choice of Amperian Loop:
The rectangular Amperian loop (at right) is chosen so that B is constant on the two sides parallel to the solenoid axis and perpendicular to the ds on the other two sides. This allows us to take B "out of the integral".
With the Amperian loop above we have
The shape of the B field due to a solenoid is the same as that of a bar magnet and a magnetic dipole.
What does a clock do when it's hungry ? It goes back four seconds.
Dr. C. L. Davis
Physics Department
University of Louisville
email: c.l.davis@louisville.edu
