
 Gauss's Law is the first of Maxwell's equations we
will consider. At first the whole concept of Gauss's Law
will seem to be very abstract and confusing,
Gauss's Law is the first of Maxwell's equations we
will consider. At first the whole concept of Gauss's Law
will seem to be very abstract and confusing,
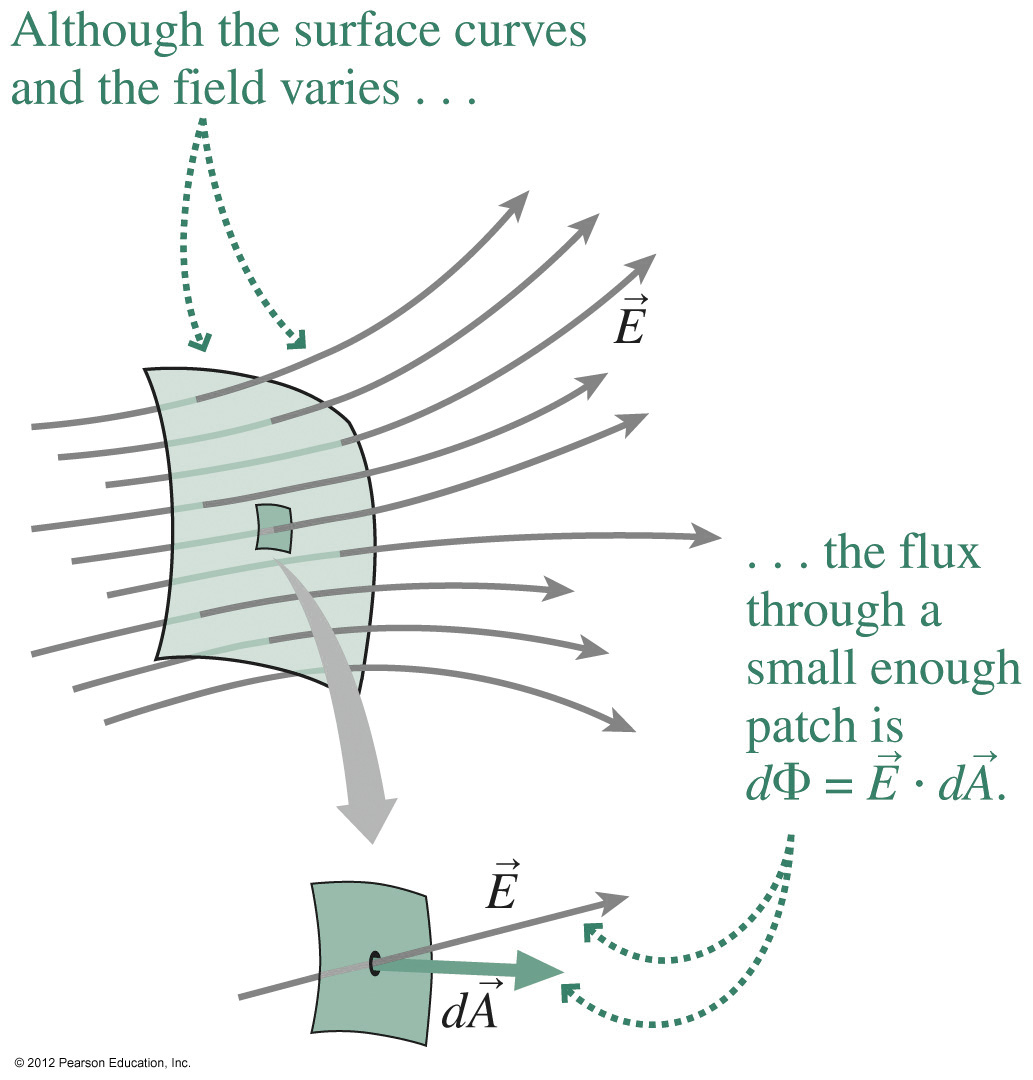 At every point on a
surface we can calculate an "element" of the electric flux
given by
At every point on a
surface we can calculate an "element" of the electric flux
given byso that the total electric flux passing through a surface, S, is given by,
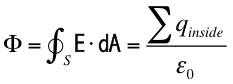
where the circle on the integral means that the surface is closed and qinside is the net charge inside this closed surface.
S1: At every point on this surface both E and dA are directed "outwards", such that the scalar product E·dA = EdAcosθ is always positive. Thus the integral over the surface S1 will be positive, as it must be if Gauss's Law is to be satisfied, since the net charge enclosed is positive.
- S2 : E is directed "inwards", dA "outwards", leading to a negative value for the flux through S2, consistent with the fact that the net charge enclosed is negative.
- S3: Some of this surface has E directed "inwards" the remainder has E directed "outwards". dA is "outwards" everywhere on the surface. Therefore the flux integral has both positive and negative contributions. Since there is no net charge enclosed by S3 by Gauss's Law the net flux will be zero.
- S4: Once again there are negative and positive contributions to the flux integral, so that we can write Gauss's Law,
Dr. C. L. Davis
Physics Department
University of Louisville
email: c.l.davis@louisville.edu
