Displacement Current

"A fact is a simple statement that everyone believes. It is innocent, unless found guilty. A hypothesis is a novel suggestion that no one wants to believe. It is guilty, until found effective"

Edward Teller

Having discussed Gauss' Law for Magnetism, we now have four equations describing electromagnetism,

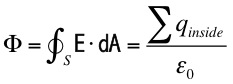
Gauss' Law: elecgausseqn3

elecgausseqn3

Ampere's Law: magampereeqn1

Faraday's Law: magfaradayeqn6

Nobody's Law:

Looking carefully at these equations, the two flux equations are now consistent with our physical understanding of electric and magnetic charges.

The line integrals are a different matter. The right hand side of Ampere's Law has a summation over electric currents. Naively we would expect a similar sum over "magnetic currents" on the right hand side of Faraday's Law. But since there are no magnetic charges, "magnetic currents" do not exist and the necessity for such an additional term disappears.

However, in words, Faraday's Law states that

"A changing magnetic field ( ) gives rise to an electric field ( )"

For a more complete correspondence between E and B we would expect a term added to the right hand side of Ampere's Law which indicates,

"A changing electric field ( ) gives rise to a magnetic field ( )"

Maxwell proposed this addition, the existence of which is now physically verified. Furthermore, Maxwell showed that this additional term, known as the displacement current, is essential for the description of electromagnetic waves.

The form of the displacement current term can be obtained by the argument described below.

We have seen that current and current density are related by the following equation

Suppose we consider a closed surface, then charge conservation tells us that this flux integral must be zero. Charge cannot be created or destroyed inside the closed surface, therefore,

This equation can be considered as a formal statement of conservation of charge.

Consider a parallel plate capacitor (at right). The closed surface over which we will apply the above integral is S₁ and S₂. Current I passes in though S₁, but since S₂ is between the capacitor plates, no current passes out of the closed surface. As it stands, we have violated conservation of charge... What to do ? Propose that there is an equal current passing out of the closed surface through S₂ - the "displacement current".

Now

magdisplacementeqn6

Therefore, if we define

as the displacement current, by writing

we can ensure charge is conserved.

Therefore, including the displacement current, Ampere's Law becomes,

This girl said she recognized me from the vegetarian club, but I'd never met herbivore.

Dr. C. L. Davis
Physics Department
University of Louisville
email: c.l.davis@louisville.edu